Belajar Bit Paritas Genap dan Ganjil Dalam Biner

Bit Paritas

Dalam sistem digital kata (word) adalah sekelompok bit yang diperlakukan, disimpan, d_an dipindahkan sebagai suatu kesatuan. Sebagai contoh, misalkan sebuah komputer 8421 akan menambahkan 0.101 1000 0011 dan 0010 0100 0110. (Ini adalah 583 dan 246.) Masing-masing bilangan BCD ini merupakan sebuah kata. Komputer membawa masing-masing kata ini keluar dari memori dan meletakkannya ke dalam satuan arit-matika. Jumlahnya merupakan sebuah kata baru yang kemudian diletakkan kembali ke dalam memori.

Pada saat kata-kata sedang dipindahkan dan disimpan, kesalahan dapat masuk ke dalam kata-kata tersebut. Sebagai contoh, salah satu 0 dalam suatu kata secara tidak di-sengaja mungkin berubah menjadi 1 akibat pemutusan sesaat, akibat derau, akibat per-alihan, dan sebagainya. Di bawah kondisi operasi normalnya perubahan semacam itu tidak mungkin terjadi, namun suatu kesalahan dapat merusakkan segalanya. Oleh karenanya, dibutuhkan metoda-metoda untuk mendeteksi kesalahan yang timbul pada saat suatu kata sedang dipindahkan atau disimpan.

Kelompok terlarang

Dalam semua sandi BCD yang dibahas sejauh ini, kita hanya mempergunakan 10 di anta-ra 16 kemungkinan kombinasi 4-bit. Oleh karenanya, salah satu cara untuk mendapat-kan kesalahan adalah mencari kombinasi-kombinasi yang tidak diperkenankan. Jika salah satu kombinasi terlarang ini muncul dalam memori, segera kita ketahui bahwa te-lah terjadi kesalahan.

Pemeriksaan kombinasi terlarang merupakan salah satu kemungkinan, namun cara ini tidak memberikan probabilitas yang cukup tinggi dalam menangkap kesalahan. Pen-dekatan yang paling luas penggunaannya untuk mendeteksi kesalahan yang timbul se-lama penyimpanan dan pemindahan kata-kata adalah membubuhkan suatu bit paritas pada kata tersebut.

Paritas Genap dan Ganjil

Paritas genap berarti membubuhkan sebuah bit tambahan kepada sekelompok bit untuk menghasilkan banyaknya I yang genap. Sebagai contoh, misalkan kita mempunyai se-buah kata seperti 0111. Terdapat tiga bush 1 dalam kata ini, banyaknya 1 yang ganjil. Kita bubuhkan sebuah 1 tambahan pada kata ini untuk mendapatkan 0 1 1 1. Sekarang banyaknya 1 menjadi genap. Kata baru ini dapat dipindahkan dan disimpan oleh kom-puter, dan dapat diperiksa paritas genapnya pada berbagai titik untuk meyakinkan bah-wa tak ada kesalahan yang telah memasuki kata tersebut.

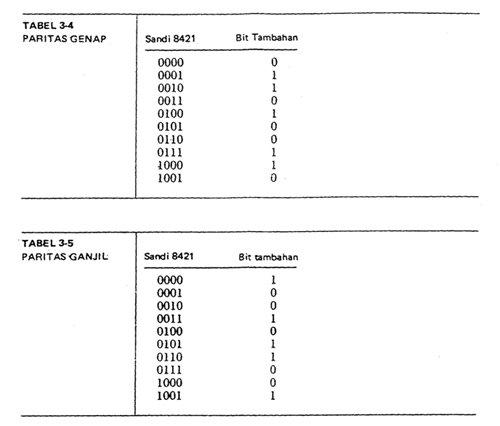
Sebagai gambaran lain bagi paritas genap, Tabel 3-4 memperlihatkan sandi 8421 dengan sebuah bit paritas-genap. Bit paritas menghasilkan banyaknya 1 yang genap bagi masing-masing kelompok sandi.

Terdapat pula paritas ganjil. Dalam hal ini, bit paritas tambahan membuat banyaknya 1 menjadi ganjil. Tabel 3-5 memperlihatkan sandi 8421 dengan sebuah bit paritas

Kedua jenis paritas ini lazim digunakan; tidak ada argumen yang kuat untuk lebih menyukai salah satu jenis.

Penggunaan bit paritas untuk mendeteksi kesalahan berdasarkan dua asumsi yang berlaku pada kebanyakan sistem digital:

Probabilitas kesalahan sangat kecil

Dalam hal suatu kesalahan masuk ke dalam sebuah kata, kesalahan tersebut hampir dapat dipastikan merupakan kesalahan 1-bit. Kemungkinan 2 atau lebih bit berubah secara tak disengaja sangatlah kecil kecuali jika terjadi gangguan total, yang akan terde-teksi oleh sarana lain.

Dengan perkataan lain, pemeriksaan paritas akan menangkap semua kesalahan 1-bit namun tidak menangkap kesalahan ganda. Dalam kebanyakan sistem digital kemung-kinan terjadi kesalahan ganda sangat kecil.

Sebagai contoh, misalkan terdapat lima buah lubang di tanah. Kemungkinan sebuah meteor jatuh ke dalam satu lubang adalah kecil. Namun kemungkinan meteor jatuh ke dalam dua lubang adalah Perneriksaan paritas khususnya lazim dilakukan dalam piranti penyimpanan seperti pita, drum, inti magnetis, serta pita kertas. Pita magnetis merupakan cara yang murah untuk menyimpan sejumlah besar informasi digital, namun lebih rentan terhadap kesalahan dibandingkan teknik-teknik lain. Kemungkinan terjadi ke'salahan ganda pada _pita magnetis lebih besar, sehingga pemeriksaan paritas-tunggal keandalannya tidak se-tingSi• pada bagian-bagian lain dalam sistem digital.

Share this post